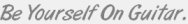Home
> Theory
> Chord Scales
Chord Scales on Guitar - Harmonising Scales Using Chords
Most guitarists learn about chords and scales, but few learn about the
intrinsic connection between the two. One way of seeing this
relationship is through chord
scales, a form of scale harmonisation.
Simply put, a chord scale is revealed when you build a chord on each degree of a scale, using related tones from within that scale.
For example, the major scale has seven degrees, and we can therefore build seven chords from that scale, one chord rooted on each degree.
This gives us a chord system compatible with the parent scale from which it's derived. Once you fully understand this relationship, you'll be able to connect scales to related chord sequences far more easily.
For example, referring to the major scale again, if the chords Cmaj, Dm and Gmaj were played, we'd know the C major scale would be compatible, because these three chords are part of the C major chord scale.
Confused? Let's delve a little deeper...
Video lesson
All we do is build chords on each degree of the major scale to give us our seven-chord scale.
Note that you'll often see Roman numerals used to represent these scale degrees - upper case numerals for the major chords, lower case for minor (and diminished) chords.
So if you see a progression written as I, IV, V, you'll know it's referring to the 1st, 4th and 5th degree chords of the scale.
ii, V, I would be the 2nd, 5th and 1st chords.
The numerals allow us to see a relationship of chords without specifying a key, because the relationship between the chords, just like the scale's intervals, is the same no matter which key you're in. It's a movable relationship, in other words.
Later, we'll go into what makes a given degree's chord major or minor. The below table will help you in transposing this system to different keys. Notice how the first chord in the scale shares the same root (as indicated by the chord letter) as its parent scale. This is known as the 1 or tonic chord of the scale.
What's great about learning this chord scale system is that, if you pull out any combination of chords in a given key, the related scale will work over every chord in that sequence. It's the system most commonly used in pop and rock music. So, when you become familiar with the scale, you'll start to pick up songs by ear much more quickly and easily.
For example, using the scale of G major, if the chord progression was Cmaj / Dmaj / Am / Gmaj, then the G major scale would work over the entire progression because all of these chords are a part of that scale.
In fact, every chord in a given scale uses notes from that parent scale. Since there are seven tones in the major scale, you potentially have seven tones from which to build a related chord. However, on guitar, chords most commonly tend to involve three to six tones.
In the table below, you can see how each degree of the scale builds a new triad based on how the intervals of that chord fall in the scale. Remember, we build chords from their root (1) notes, so when building a chord on a scale degree, that degree's note becomes the root note of the chord (e.g. Cmaj = C, Dm = D, Em = E etc.)
So why are some chords in the scale major and others minor? Because the intervals of the scale dictate whether a major 3rd (3) or minor 3rd (b3) can be used above a given degree's root.
Because all these chords use notes from the C major scale, we could theoretically play a C major based solo over any combination of these chords, even if C major itself is not in the progression.
The first is to simply build open position chords and/or barre chords on each degree of the scale. Using C major as our example again, we could lay out the intervals of the scale across the lowest two strings (E and A). These two strings give us the bass root notes for the most common barre chord forms, often referred to as the E shape and A shape.

So our C major scale root (1) is on the note C, and this is where our tonic chord would be rooted, whether we use an E form barre chord at the 8th fret or an open C major form at the 3rd fret.
The other way is to pull chord shapes right out of a scale pattern. This method gives you a wider selection of chord voicings to choose from. Here's how we do it...
When learning scales, you'll learn some patterns/positions for playing that scale on the fretboard.
For example, here are the first two positions of the major scale combined...
From this we can identify the scale degrees and build chords around those degrees. This is where it's beneficial to know your basic intervals from a starting/root note (e.g. minor 3rd, major 3rd, perfect 5th etc.) across multiple strings.
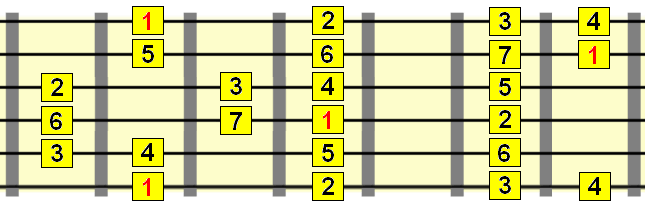
For example, we know from earlier that the 2nd degree builds a minor chord, so we could use the pattern of the parent C major scale to provide the necessary intervals for that chord (and the other degree chords). The 2 of C major becomes the root (1) note of its ii chord, D minor...
So whichever key you choose to play in, match up the scale's root to your chosen key (e.g. in E major, the root would be... E) and build the chord scale from that root, remembering that the 1st chord in the scale (I) shares the root note of the parent scale (E major scale, E major I chord).
Test yourself in different keys. Refer to the tables from earlier if you get stuck!
As mentioned earlier, a lot of popular music uses this chord scale system, so the more you train your ear to hearing, as well as visualising these chord relationships across multiple keys, the easier it'll be to pick up songs by ear and know when a scale can be used over an entire progression, or when you need to change scales.
In the next part we'll look at how we can build extended chords (up until now we've only been building triads, three-note chords), still using the degrees and notes of the parent scale.
More Guitar Theory Lessons
Chord Scales on Guitar - Harmonising Scales Using Chords
Most guitarists learn about chords and scales, but few learn about the
intrinsic connection between the two. One way of seeing this
relationship is through chord
scales, a form of scale harmonisation.

|
Simply put, a chord scale is revealed when you build a chord on each degree of a scale, using related tones from within that scale.
For example, the major scale has seven degrees, and we can therefore build seven chords from that scale, one chord rooted on each degree.
This gives us a chord system compatible with the parent scale from which it's derived. Once you fully understand this relationship, you'll be able to connect scales to related chord sequences far more easily.
For example, referring to the major scale again, if the chords Cmaj, Dm and Gmaj were played, we'd know the C major scale would be compatible, because these three chords are part of the C major chord scale.
Confused? Let's delve a little deeper...
Video lesson
Basic Theory Behind Chord Scales
As mentioned above, the major scale is one parent scale in which a chord scale system resides.All we do is build chords on each degree of the major scale to give us our seven-chord scale.
| Degree | 1 I |
2 ii |
3 iii |
4 IV |
5 V |
6 vi |
7 vii |
| Chord | Maj | min | min | Maj | Maj | min | dim |
Note that you'll often see Roman numerals used to represent these scale degrees - upper case numerals for the major chords, lower case for minor (and diminished) chords.
So if you see a progression written as I, IV, V, you'll know it's referring to the 1st, 4th and 5th degree chords of the scale.
ii, V, I would be the 2nd, 5th and 1st chords.
The numerals allow us to see a relationship of chords without specifying a key, because the relationship between the chords, just like the scale's intervals, is the same no matter which key you're in. It's a movable relationship, in other words.
Later, we'll go into what makes a given degree's chord major or minor. The below table will help you in transposing this system to different keys. Notice how the first chord in the scale shares the same root (as indicated by the chord letter) as its parent scale. This is known as the 1 or tonic chord of the scale.
| Degree ► Scale ▼ |
I | ii | iii | IV | V | vi | vii |
| C Major | Cmaj | Dm | Em | Fmaj | Gmaj | Am | Bdim |
| C# Major | C#maj | D#m | Fm | F#maj | G#maj | A#m | Cdim |
| D Major | Dmaj | Em | F#m | Gmaj | Amaj | Bm | C#dim |
| Eb Major | Ebmaj | Fm | Gm | Abmaj | Bbmaj | Cm | Ddim |
| E Major | Emaj | F#m | G#m | Amaj | Bmaj | C#m | D#dim |
| F Major | Fmaj | Gm | Am | Bbmaj | Cmaj | Dm | Edim |
| F# Major | F#maj | G#m | A#m | Bmaj | C#maj | D#m | E#dim |
| G Major | Gmaj | Am | Bm | Cmaj | Dmaj | Em | F#dim |
| Ab Major | Abmaj | Bbm | Cm | Dbmaj | Ebmaj | Fm | Gdim |
| A Major | Amaj | Bm | C#m | Dmaj | Emaj | F#m | G#dim |
| Bb Major | Bbmaj | Cm | Dm | Ebmaj | Fmaj | Gm | Adim |
| B Major | Bmaj | C#m | D#m | Emaj | F#maj | G#m | A#dim |
What's great about learning this chord scale system is that, if you pull out any combination of chords in a given key, the related scale will work over every chord in that sequence. It's the system most commonly used in pop and rock music. So, when you become familiar with the scale, you'll start to pick up songs by ear much more quickly and easily.
For example, using the scale of G major, if the chord progression was Cmaj / Dmaj / Am / Gmaj, then the G major scale would work over the entire progression because all of these chords are a part of that scale.
In fact, every chord in a given scale uses notes from that parent scale. Since there are seven tones in the major scale, you potentially have seven tones from which to build a related chord. However, on guitar, chords most commonly tend to involve three to six tones.
Major Scale Triads
Let's use the C major scale for the following example.In the table below, you can see how each degree of the scale builds a new triad based on how the intervals of that chord fall in the scale. Remember, we build chords from their root (1) notes, so when building a chord on a scale degree, that degree's note becomes the root note of the chord (e.g. Cmaj = C, Dm = D, Em = E etc.)
- Major triad = 1, 3, 5 (major 3rd and perfect 5th intervals from the root)
- Minor triad = 1, b3, 5 (minor 3rd and perfect 5th intervals from the root)
- Diminished triad = 1, b3, b5 (minor 3rd, diminished 5th intervals from the root)
| Scale Notes ► Chords ▼ |
C | D | E | F | G | A | B |
| Cmaj (C E G) | 1 | 3 | 5 | ||||
| Dm (D F A) | 1 | b3 | 5 | ||||
| Em (E G B) | 1 | b3 | 5 | ||||
| Fmaj (F A C) | 5 | 1 | 3 | ||||
| Gmaj (G B D) | 5 | 1 | 3 | ||||
| Am (A C E) | b3 | 5 | 1 | ||||
| Bdim (B D F) | b3 | b5 | 1 |
So why are some chords in the scale major and others minor? Because the intervals of the scale dictate whether a major 3rd (3) or minor 3rd (b3) can be used above a given degree's root.
Because all these chords use notes from the C major scale, we could theoretically play a C major based solo over any combination of these chords, even if C major itself is not in the progression.
| Struggling with mastering intervals on guitar? You can now download interactive software to help you learn all the essential fretboard theory you need to dominate the fretboard. Learn more here |
Visualising Chord Scales on the Guitar Fretboard
The above tables are great as far as general music theory goes, but how do we visualise all this on the guitar fretboard? There are a couple of ways...The first is to simply build open position chords and/or barre chords on each degree of the scale. Using C major as our example again, we could lay out the intervals of the scale across the lowest two strings (E and A). These two strings give us the bass root notes for the most common barre chord forms, often referred to as the E shape and A shape.

So our C major scale root (1) is on the note C, and this is where our tonic chord would be rooted, whether we use an E form barre chord at the 8th fret or an open C major form at the 3rd fret.
The other way is to pull chord shapes right out of a scale pattern. This method gives you a wider selection of chord voicings to choose from. Here's how we do it...
When learning scales, you'll learn some patterns/positions for playing that scale on the fretboard.
For example, here are the first two positions of the major scale combined...

From this we can identify the scale degrees and build chords around those degrees. This is where it's beneficial to know your basic intervals from a starting/root note (e.g. minor 3rd, major 3rd, perfect 5th etc.) across multiple strings.
For example, we know from earlier that the 2nd degree builds a minor chord, so we could use the pattern of the parent C major scale to provide the necessary intervals for that chord (and the other degree chords). The 2 of C major becomes the root (1) note of its ii chord, D minor...

So whichever key you choose to play in, match up the scale's root to your chosen key (e.g. in E major, the root would be... E) and build the chord scale from that root, remembering that the 1st chord in the scale (I) shares the root note of the parent scale (E major scale, E major I chord).
Test yourself in different keys. Refer to the tables from earlier if you get stuck!
As mentioned earlier, a lot of popular music uses this chord scale system, so the more you train your ear to hearing, as well as visualising these chord relationships across multiple keys, the easier it'll be to pick up songs by ear and know when a scale can be used over an entire progression, or when you need to change scales.
In the next part we'll look at how we can build extended chords (up until now we've only been building triads, three-note chords), still using the degrees and notes of the parent scale.
| |
Tweet |
 Like This?
Subscribe & Learn More... Like This?
Subscribe & Learn More...Subscribe to the fretjam newsletter below for updates and extras, plus grab your free copy of Uncommon Chords: 101 Vibrant Voicings You Won't Find on a Typical Chord Chart. |
Part 2 Coming Soon
More Guitar Theory Lessons