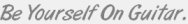Home
> Theory
> Sharps
and Flats
You've probably heard the terms "sharp" and "flat" being used by musicians, but perhaps aren't quite sure what they mean.
Knowing this stuff will come in handy when you start studying the fretboard in more detail.
Take a look at the scale pattern below...
Intervals: 1 2 3 4 5 6 7
This scale is known as the major scale. Now, there's a separate lesson on this scale, but we're going to reference it in this lesson because of how fundamental this scale is to music theory.
The major scale can be seen as a scale with no sharp or flat intervals - simply 1 2 3 4 5 6 7. The major scale, therefore, is our starting point, our foundation for creating any other scale as well as being a scale in its own right (and used a lot in music).
In other words, we widen or narrow intervals from their original major scale positions to create new scales. The movement of these intervals creates sharps (♯) and flats (♭) (note: I'm lazy so I tend to just type a b for flat, but the actual symbol is a more stylised ♭. Also, it's common to use a standard # hash for sharp, but the proper symbol is ♯).
An example...
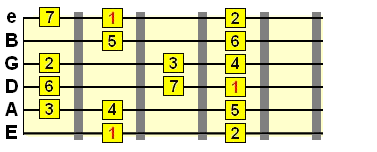
Let's say we moved the 7th tone of the major scale down one fret position. In music theory, that's known as a flat 7th or minor 7th (♭7). We've flattened/lowered the 7th by one semitone/half step, giving us a new, flat 7th scale...
Intervals: 1 2 3 4 5 6 ♭7
Incidentally, that flat 7th scale has its own name, Mixolydian, but with only one tone difference from the elementary major scale.
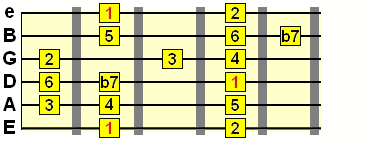
Going back to the original major scale pattern, we could sharpen a tone, such as the 4th. This is like the opposite of flattening a tone, so we move it up one fret/semitone/half step this time, creating a sharp 4th (♯4) scale, also known as Lydian...
Intervals: 1 2 3 ♯4 5 6 7
So, the first thing to remember is that sharps and flats can be seen as referenced against their original position in the major scale. That is why the major scale is so important in music.
This means that if you see the symbol ♭2 used in a scale sequence, you'll know it's a flat/minor 2nd interval.
Even minor scales can be seen as referenced against the major scale - the minor 3rd is simply a flat 3rd (♭3), which means the major 3rd interval (3) of the major scale has been flattened by one semitone/half step.
As you work/play your way through the scales section on this site, you'll come across various combinations of sharps and flats, which is what gives a scale its unique sound.
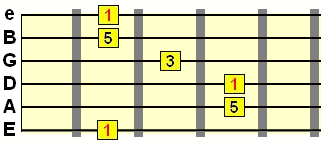
Take a basic major triad, which consists of the root (1st), 3rd and 5th tones from the major scale. Here's a very typical chord shape for the major triad (an E shape barre chord)...
If we flatten the 3rd, we get a minor triad - 1, ♭3, 5.
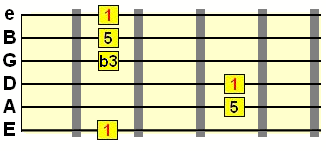
So, just like with scales, when a chord tone is flattened, it is simply moved down one semitone/half step (the equivalent of one fret position).
And of course, there are other sharp/flat tone chords, such as this jazzy flat 5th and flat 7th chord...
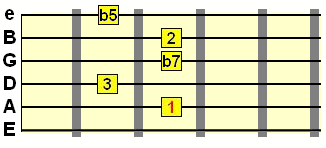
Intervals: 1 2 3 ♭5 ♭7
If you were to superimpose a major scale pattern over that chord shape, you can (hopefully) see how this chord has been formed (clue: the 7 and 5 have been altered)...
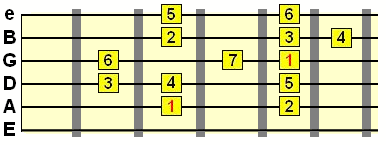
So by starting with the major scale as our foundation, we can see that all sharps and flats are positioned in relation to it.
You can learn more about building chords, arpeggios and scales in other lessons on this site. This specific lesson is just about understanding where sharps and flats come from!
Now, you could actually call F sharp "G flat", because it's the same note (enharmonic). You could also call B flat "A sharp" - again, the same note.
So what makes a specific note sharp or flat? It's all about the context in which the note is used.
Firstly, we use sharps or flats to make reading a sequence of notes in a scale easier.
For example, if we were spelling out a scale which included the note A, we would rarely use Ab along side it, because that would mean the presence of two As. We'd therefore use its enharmonic G♯ instead.
Secondly, we use sharps or flats for consistency. Try not to mix sharps and flats. For example...
E flat major scale...
E♭ F G A♭ B♭ C D
C sharp major scale...
C♯ D♯ E♯ F♯ G♯ A♯ B♯
Notice how we use B♯ instead of a natural C, because of that first "rule" of only using a note letter once, and we're already using C♯.
So you can see that by ensuring each note letter is different, and consistently using sharps or flats in a scale's notation, we can make the spelling of scales clearer and easier on the eye. It also has a significant function in musical notation (but it's not absolutely necessary to learn that as you'll realise!)
Guitar Fretboard Lessons
Guitar Theory Lessons
Sharps and Flats on Guitar Explained
This lesson will help you understand what sharps (♯) and flats (♭) are in music, where they come from and how they appear on guitar.You've probably heard the terms "sharp" and "flat" being used by musicians, but perhaps aren't quite sure what they mean.
Knowing this stuff will come in handy when you start studying the fretboard in more detail.
Sharps and flats in guitar scales
The best way to understand the role of sharps and flats in music theory is to observe how they appear in relation to scales - a sequence of intervals relative to a root (1) note.Take a look at the scale pattern below...

Intervals: 1 2 3 4 5 6 7
This scale is known as the major scale. Now, there's a separate lesson on this scale, but we're going to reference it in this lesson because of how fundamental this scale is to music theory.
The major scale can be seen as a scale with no sharp or flat intervals - simply 1 2 3 4 5 6 7. The major scale, therefore, is our starting point, our foundation for creating any other scale as well as being a scale in its own right (and used a lot in music).
In other words, we widen or narrow intervals from their original major scale positions to create new scales. The movement of these intervals creates sharps (♯) and flats (♭) (note: I'm lazy so I tend to just type a b for flat, but the actual symbol is a more stylised ♭. Also, it's common to use a standard # hash for sharp, but the proper symbol is ♯).
An example...
Let's say we moved the 7th tone of the major scale down one fret position. In music theory, that's known as a flat 7th or minor 7th (♭7). We've flattened/lowered the 7th by one semitone/half step, giving us a new, flat 7th scale...

Intervals: 1 2 3 4 5 6 ♭7
Incidentally, that flat 7th scale has its own name, Mixolydian, but with only one tone difference from the elementary major scale.
Going back to the original major scale pattern, we could sharpen a tone, such as the 4th. This is like the opposite of flattening a tone, so we move it up one fret/semitone/half step this time, creating a sharp 4th (♯4) scale, also known as Lydian...

Intervals: 1 2 3 ♯4 5 6 7
So, the first thing to remember is that sharps and flats can be seen as referenced against their original position in the major scale. That is why the major scale is so important in music.
This means that if you see the symbol ♭2 used in a scale sequence, you'll know it's a flat/minor 2nd interval.
Even minor scales can be seen as referenced against the major scale - the minor 3rd is simply a flat 3rd (♭3), which means the major 3rd interval (3) of the major scale has been flattened by one semitone/half step.
As you work/play your way through the scales section on this site, you'll come across various combinations of sharps and flats, which is what gives a scale its unique sound.
Sharps and flats in guitar chords
Just like with scales, sharps and flats exist within certain chord forms. Think of chords as a group of tones pulled out of a scale - that way, you'll better understand how the sharps and flats in chords can be connected to a scale with the same intervals - crucial for being able to select your notes for a solo.Take a basic major triad, which consists of the root (1st), 3rd and 5th tones from the major scale. Here's a very typical chord shape for the major triad (an E shape barre chord)...

If we flatten the 3rd, we get a minor triad - 1, ♭3, 5.

So, just like with scales, when a chord tone is flattened, it is simply moved down one semitone/half step (the equivalent of one fret position).
And of course, there are other sharp/flat tone chords, such as this jazzy flat 5th and flat 7th chord...

Intervals: 1 2 3 ♭5 ♭7
If you were to superimpose a major scale pattern over that chord shape, you can (hopefully) see how this chord has been formed (clue: the 7 and 5 have been altered)...

So by starting with the major scale as our foundation, we can see that all sharps and flats are positioned in relation to it.
You can learn more about building chords, arpeggios and scales in other lessons on this site. This specific lesson is just about understanding where sharps and flats come from!
Sharp and flat notes on the fretboard
In the fretboard lessons, we learned where the notes lie on the fretboard. We also learned the natural sequence of notes from E to E...E | F | F♯ | G
| A♭ | A | B♭ | B
| C | C♯ | D | E♭ | E
Now, you could actually call F sharp "G flat", because it's the same note (enharmonic). You could also call B flat "A sharp" - again, the same note.
So what makes a specific note sharp or flat? It's all about the context in which the note is used.
Firstly, we use sharps or flats to make reading a sequence of notes in a scale easier.
For example, if we were spelling out a scale which included the note A, we would rarely use Ab along side it, because that would mean the presence of two As. We'd therefore use its enharmonic G♯ instead.
Secondly, we use sharps or flats for consistency. Try not to mix sharps and flats. For example...
E flat major scale...
E♭ F G A♭ B♭ C D
C sharp major scale...
C♯ D♯ E♯ F♯ G♯ A♯ B♯
Notice how we use B♯ instead of a natural C, because of that first "rule" of only using a note letter once, and we're already using C♯.
So you can see that by ensuring each note letter is different, and consistently using sharps or flats in a scale's notation, we can make the spelling of scales clearer and easier on the eye. It also has a significant function in musical notation (but it's not absolutely necessary to learn that as you'll realise!)
| |
Tweet |
 Like This?
Subscribe & Learn More... Like This?
Subscribe & Learn More...Subscribe to the fretjam newsletter below for updates and extras, plus grab your free copy of Uncommon Chords: 101 Vibrant Voicings You Won't Find on a Typical Chord Chart. |
Related
Guitar Fretboard Lessons
Guitar Theory Lessons